Module 2.2: Surface Interpolation

In this week's lab, I investigated different surface interpolation techniques using ArcGIS Pro including Thiessen, Inverse Distance Weighted (IDW) and Spline (Regularized and Tension). Each interpolation technique has its advantages and disadvantages and choosing which to use is dependent on the type, number and purpose of the data being used in the analysis.

For this analysis, I used a data set of water quality samples taken in Tampa Bay, focusing on Biochemical Oxygen Demand (BOD) in milligrams per liter.

The first technique I explored was the Thiessen technique. This interpolation technique assigns an interpolated value equal to the value found at the nearest sample point. It is widely used because it is easy to create, use and interpret. In fact, no GIS software is required for the creation of the polygons. The results in this lab analysis indicate that the statistics generated from the Thiessen technique are almost the same as non-spatial techniques. However, the Thiessen technique creates a series of polygons with oddly shaped boundaries and abrupt transitions as seen in the image below. The resulting surface may not show well defined boundaries of a specific area. In fact, in this lab, the resulting surface was square, which is not representative of the boundary of the sample area and would have to be clipped to the area of study for a map. This technique would not be suitable for continuous variables as gradual changes in data would not be represented.



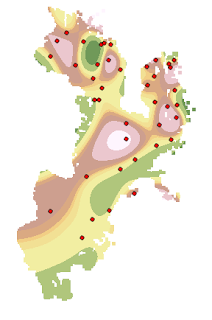
The second technique was the Inverse Distance Weighted or IDW. In this technique, the sampling point has a local influence that diminishes with distance, meaning that points closer together are weighted more than those further away. IDW assumes that points closer together will have the same value than those further away. The image below is the IDW interpolation for the same Tampa Bay water quality data.

The final technique was the Spline. This technique uses polynomial functions to minimize the surface curvature, resulting in a surface that passes exactly through the input points. In this analysis, I used both regularized and tension spline analyses. Both the regularized and tension techniques use the same calculation principle to derive the surface area, but the tension method is more restrictive and keeps the values closer to the original point. The images below show the Spline interpolations using the regularized (top) and tension (bottom) techniques for the same Tampa Bay water quality data.

Spline - Regularized

Spline - Tension






Comments

Post a Comment

Popular posts from this blog

Module 2: Coordinate Systems

Image
In this week's lab I explore different coordinate systems and projections in order to better understand the nature of distortions introduced by the systems. For the last part of the lab, I was tasked with selecting a state in the contiguous US and selecting an appropriate projection for the area. I selected the state of Wyoming as my area of interest. Wyoming has 4 State Plane zones and two UTM zones, so neither a single State Plane nor UTM system would work for this area without distorting the size or shape of the state. Therefore, the best coordinate system for this area is Custom Coordinate system. I chose NAD 1983 WyLam (Meters), a custom system specifically for the state of Wyoming, as the projected coordinate system. This coordinate system is a Lambert secant-case normal-aspect conic type projection which preserves shape and is appropriate for a general reference map. The standard parallels are placed at 41N and 45N, the boundaries of the state of Wyoming, which minimizes...
Read more

Module 6: Proportional Symbol and Bivariate Choropleth Mapping

Image
The objectives of this week's lab was to explore proportional symbol and bivariate choropleth mapping techniques, as well as customizing legends for each technique. One of the data sets for this lab included positive and negative values. The final map utilizes proportional symbols to show both positive and negative values. This map is essentially two proportional symbol maps overlaid on each other, one for positive job growth and another for negative job growth, with the symbols for both variables sized the same. Utilizing proportional symbols to show both positive and negative values is an effective way to visualize areas that show the greatest and lowest values. These areas are easy to see quickly on the map and give the map reader a simple way to visualize the variable being mapped. Fig 1. Proportional symbol map using positive and negative values.  Another data set for this lab examined contained two data variables: percent of the US population in each state that is obe...
Read more

Module 8: Isarithmic Mapping

Image
The purpose of this lab was to investigate the PRISM Interpolation Method to develop an isarithmic map of average annual precipitation for Washington state. PRISM is a model that calculates climate-elevation relationships from point data for each grid cell in a digital elevation model (DEM). The data set for Washington state includes annual precipitation over a 30 year period (1981-2010). In this lab, I explored two methods for symbolizing this data in ArcGIS Pro. The first symbolization method was using continuous tone symbology. Continuous tone symbology symbolizes a feature with differing shades between contours, where each point on the surface is shaded with a tone proportional to the value of the surface at that point. This results in a map where the shade of the colors vary and blend between contours, creating a smooth surface. A hillshade effect was applied to the map by using the Dynamic Range Adjustment (DRA) Hillshade Effect and editing the color and transparency of a co...
Read more